【Unityシェーダ入門】フォン鏡面反射で金属っぽくしてみる

前回はライティングの基本となるランバート拡散照明モデルを紹介しました。今回は、ランバート拡散照明モデルを応用した、フォン（Phong）鏡面反射モデルをUnityを使いながら紹介します。フォン鏡面反射は反射光を再現した照明モデルで、金属のような質感の表現に向いています。

f:id:nn_hokuson:20161104105257p:plain

今回のコンテンツは次のとおりです。

フォン鏡面反射モデルとは
反射光の計算方法
Unityでフォン反射を作成する下準備をする
シェーダとマテリアルを作る
フォン鏡面反射モデルのシェーダを書く
ブリンフォン（Blinn-Phong）鏡面反射モデル
参考文献

フォン鏡面反射モデルとは

金属など、表面がつるつるした物体に強い光が当たると、一箇所が「キラーン」と強く光ります。これをハイライトと呼び、このハイライトを再現したライティングモデルをフォン鏡面反射モデルと呼びます。

このフォン鏡面反射モデルはランバート拡散照明モデルに、ハイライトの色を単純に足し合わせたものです。

f:id:nn_hokuson:20161102203616j:plain

このハイライトの反射光をどのようにして再現するかが、この記事のポイントです。

反射光の計算方法

物体に光が当たると物体の表面で光が反射します。光が反射する方向は、物体の法線を挟んで反対方向になります。この反射ベクトルをR（reflection）とします。

f:id:nn_hokuson:20161102205137p:plain

視線がこの反射ベクトルの方向に近ければ近いほど、反射光も強くなります。言い換えれば、反射ベクトルRと視線ベクトルviewDirのなす角度θが小さければ小さいほど、反射光は強くなります。

f:id:nn_hokuson:20161102205834p:plain

反射ベクトルと視線ベクトルのなす角度は2つのベクトルの内積をとることで、次式のように求められます。両者のなす角度が0のときには、反射光の強度はcos0=1になり、反射ベクトルと視線ベクトルが離れるに従って反射光の強度も小さくなります。

R * viewDir = |R||viewDir| cosθ = cosθ

このように、反射光の強さをもとめるためには、光の反射ベクトルと視線ベクトルの内積をとれば良いことがわかりました。

では、実際にUnityを使ってフォン鏡面反射モデルを実現してみましょう。オブジェクトの配置〜シェーダファイルの作成までは前回の記事とほぼ同様です。

nn-hokuson.hatenablog.com

Unityでフォン反射を作成する下準備をする

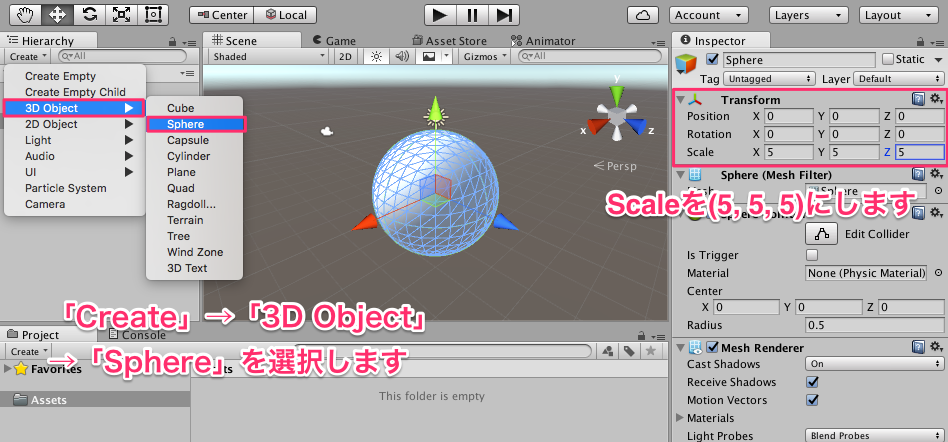
Unityのヒエラルキービューから「Create」→「3D Object」→「Sphere」を選択します。インスペクタから、作成した球のScaleを(5, 5, 5)にします。

f:id:nn_hokuson:20161101201049p:plain

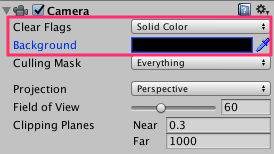
ヒエラルキービューから「Main Camera」を選択し、インスペクタから「Clear Flags」を「Solid Color」にし、「Background」を黒色にします。

f:id:nn_hokuson:20161101202057p:plain

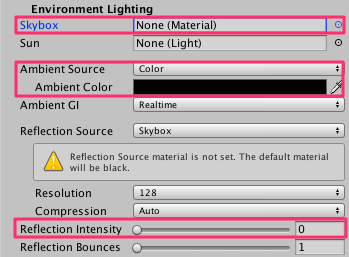
まだ、球に空の色が反映されているので、それも切りましょう。メニューバーから「Window」 →「Lighting」を選択し、「Skybox」を「None」に変更、「Ambient Source」を「Color」、「Ambient Color」を黒色、「Reflection Intensity」も「0」に設定します。

f:id:nn_hokuson:20161101203227p:plain

これで、純粋にライトからだけの影響を受けるステージができました。

シェーダとマテリアルを作る

続いてフォン鏡面反射用のシェーダを作ります。プロジェクトビューで「右クリック」→「Create」→「Shader」→「Standard Surface Shader」を選択し、作成したファイル名をSimplePhongに変更します。続いてこのシェーダファイルをアタッチするマテリアルも作成しましょう。SimplePhongを選択した状態で「右クリック」→「Create」→「Material」を選択すると、SimplePhongというマテリアルが作成されます。

f:id:nn_hokuson:20161102211458p:plain

このマテリアルを球にアタッチします。プロジェクトビューからSimpleLambertのマテリアルを選択し、シーンビューのShpereにドラッグしてください。見た目は変わりませんが、Sphereのマテリアルが「Custom/SimplePhong」になっていることを確認して下さい。

f:id:nn_hokuson:20161102211720p:plain

フォン鏡面反射モデルのシェーダを書く

では、SimpleLambertのシェーダファイルを開いて次のプログラムを入力してください。

Shader "Custom/Phong" {

	SubShader {
		Tags { "RenderType"="Opaque" }
		LOD 200
		
		CGPROGRAM
		#pragma surface surf SimplePhong
		#pragma target 3.0

 		struct Input {
			float2 uv_MainTex;
		};
 

		void surf (Input IN, inout SurfaceOutput  o) {
			o.Albedo = fixed4(1,1,1,1);
		}

		half4 LightingSimplePhong(SurfaceOutput s, half3 lightDir, half3 viewDir, half atten)
		{
			 half NdotL = max(0, dot (s.Normal, lightDir));
			 float3 R = normalize( - lightDir + 2.0 * s.Normal * NdotL );
			 float3 spec = pow(max(0, dot(R, viewDir)), 10.0);

			 half4 c;
			 c.rgb = s.Albedo * _LightColor0.rgb * NdotL + spec +  fixed4(0.1f, 0.1f, 0.1f, 1);
			 c.a = s.Alpha;
			 return c;
		}
		ENDCG
	}
	FallBack "Diffuse"
}