フラグメントシェーダのプログラムだけで円や四角形、市松模様などの図形を描くことができます。ここではUnityで使うことを想定して、フラグメントシェーダで描ける図形を10種類集めてみました。図形を作るための方法も解説しているので、参考になればと思います。
フラグメントシェーダでかけるのは単純な図形だけですが、簡単な図形でも組み合わせ方によっては株札みたいでカッコ良くなりますよ。

今回紹介するフラグメントシェーダで描ける図形には次のようなものがあります。10種類といいつつ、アニメーションも混じっていますが、そこは大目に見て下さい(^^;)
- シェーダを作る準備をする
- 2色に塗り分ける
- 線を引く
- 円を描く
- アンチエイリアスな円
- 輪を描く
- 輪の数を増やす
- 輪を動かす
- ストライプを書く
- 市松模様を描く
- 四角を描く
- 図形を複製してパターンを描画する
シェーダを作る準備をする
まずは、シェーダで図形を描く準備から始めましょう。プロジェクトを作成後、ヒエラルキービューからCreate → 3D → Planeを選択して下さい。
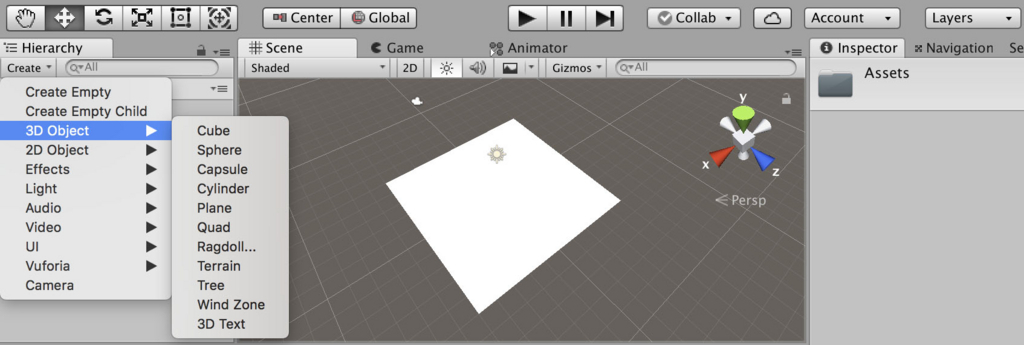
続けて、シェーダファイルを作りましょう。プロジェクトウィンドウで右クリックし、Create → Shader → Unlit Shaderを選択してフォイル名はtestにしておきます。
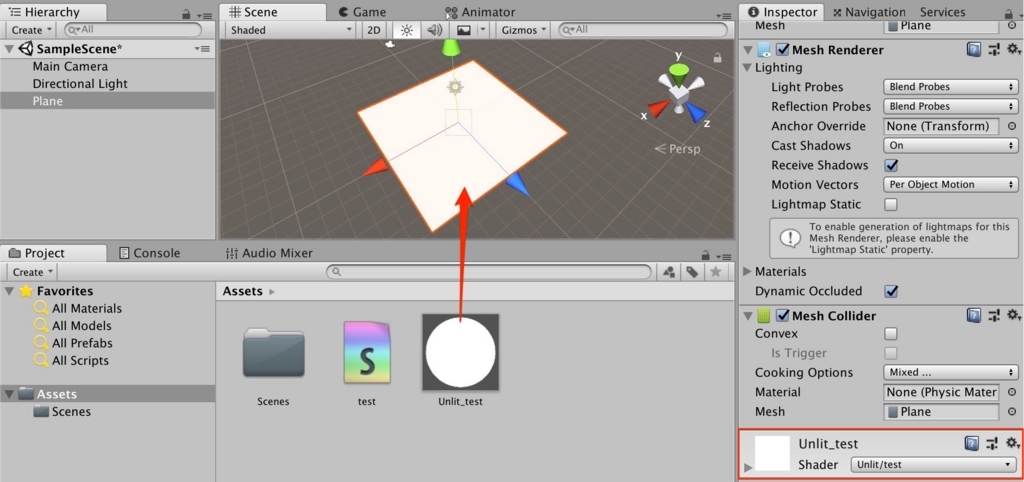
また、作成したシェーダに対応するマテリアルを作成するため、いま作成したtestシェーダを選択した状態で右クリックし、Create → Materialを選択して下さい。

最後に、いま作成したマテリアルをPlaneにドラッグ&ドロップしてアタッチしておきましょう。これでフラグメントシェーダで図形を描画する準備ができました。次からは、いま作成したtest.shaderの中のfrag関数をを書き換えていきます。
2色に塗り分ける

まずは、フラグメントシェーダを使って上のように画面を2色で塗り分ける方法を紹介します。先ほどのtest.shaderを開いてfragメソッドの中身を書き換えていきます。ここでは書き換えるフラグメントシェーダの部分のプログラムのみ載せています。
fixed4 frag (v2f i) : SV_Target { return step(0.3, i.uv.x); }
画面を2色で塗り分けるにはstep関数を使います。step関数はstep(t, x)という形で使用し、xの値がtよりも小さい場合には0、大きい場合には1を返します。
図にすると次のような感じです。簡単ですね。上の例ではt=0.3なので、xが0.3未満のところは0に、0.3以上のところは1になっています。
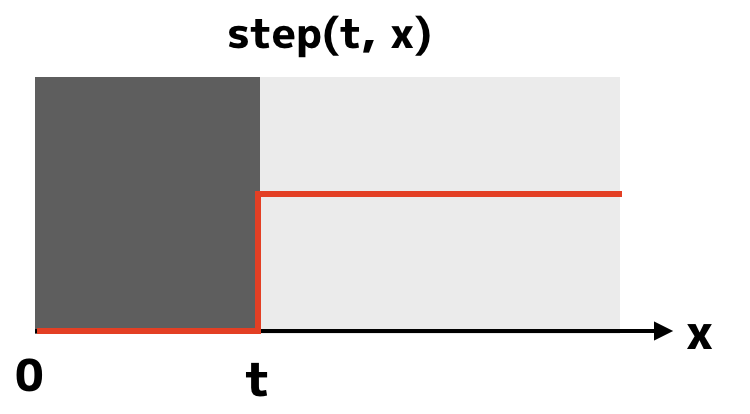
step関数の返り値によって色を付けると、様々な表現ができるようになります。返り値によって色を変えるプログラムは次のようになります。
fixed4 frag (v2f i) : SV_Target { fixed4 red = fixed4(1,0,0,1); fixed4 brown = fixed4(0.5,0.2,0.1,1); return lerp(red, brown,step(0.3, i.uv.x)); }
step関数の返り値によって色を分けるために、lerp関数を使っています。lerpはlerp(a,b,v)という形で使用します。vは0.0〜1.0で指定して、その割合によってaとbがブレンドされます。
stepの返り値は0か1なので、必ずaかbのどちらかの値が使われることになります。
頑張ればロスコっぽい絵なども作れるので挑戦してみて下さい。
線を引く

次にシェーダを使って線を引く方法を紹介します。フラグメントシェーダで線を引くのも、上と同じstep関数だけで行うことができます。
プログラムは次のようになります。
fixed4 frag (v2f i) : SV_Target { return step(0.3, i.uv.x) * step(0.69, 1.0-i.uv.x); }
今回はstepを2つ掛け合わせることで線を描画しています。2つ目のstep関数のxの値ですが、1.0から引いていることに注目してください。
これによって見かけ上、(1, 0)に原点があるようにみえます。つまり、step関数のグラフを横方向にひっくり返した形になります。

この2つをかけ合わせると・・・・
両方のグラフの値が1の部分のみ1になるので、ここが線として表示されるわけですね。

線を縦方向だけでなく横方向にも引くことで、モンドリアンっぽくなります。横方向に線を引くには上のプログラムのp.xの部分をp.yに変えればOKです。
円を描く

フラグメントシェーダで円を描くのはとても簡単で、これまでと同じくstep関数をつかいます。プログラムは次のとおりです。
fixed4 frag (v2f i) : SV_Target { fixed radius = 0.4; fixed r = distance(i.uv, fixed2(0.5,0.5)); return step(radius, r); }
画面の中心から半径r未満の座標は1、それ以上の座標では0にします。そのため、distance関数で画面中心(0.5,0.5)からの距離を調べて、step関数で半径r未満なら0、r以上なら1にしています。

円を描く位置を変えたい場合は(0.5,0.5)を変更すれば、円の中心座標を変えることが出来ます。直線よりも理解しやすいですね〜。
アンチエイリアスな円
非常に簡単に描ける円ですが、拡大してみるとエッジの部分が少しギザギザしていてきたないですね。これはエイリアシングといって、これはピクセルを1か0で描いているためエッジが目立ってしまうことが原因です。

エイリアシングの対策として、エッジの周辺をぼやかすアンチエイリアスという技術があります。ここではエッジ付近を0/1で描画するのではなく、グレースケールを考慮した値で描画する方法を紹介します。
プログラムは次のとおりです。
fixed4 frag (v2f i) : SV_Target { fixed radius = 0.4; fixed r = distance(i.uv, fixed2(0.5,0.5)); return smoothstep(radius, radius+0.02, r); }
ここではstep関数の代わりにsmoothstep関数を使っていることに注意してください。smoothstep関数はsmoothstep(a,b,x)の形で使います。xの値がa以下のときは0、b以上のときは1、aとbの間のときは0と1の間で線形補間されます。図にするとこんな感じです。
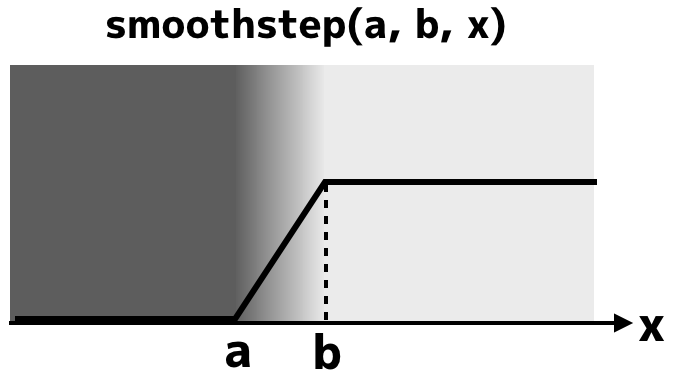
このように、step関数と比べるとsmoothstepのほうが、明暗の変化が少しなだらかに変化するわけです。
このsmoothstep関数を使ってアンチエイリアスをかけた円は、先程の例と比べるとエッジ付近がきれいに表示されていることがわかると思います。
輪を描く

輪(円の輪郭線)は直線と同じようにstep関数を2回使っても描くことができます。だんだんイメージできるようになってきましたか〜。
ただ、step関数にもすこし飽きてきたので(^^;)ここではsin関数を使って円の輪郭線を描く方法を紹介したいと思います。
sin波は次のような形をしているので、頂上の一部だけを切り取ると輪を描くことができます。2Dでイメージしにくい場合は3Dで考えると分かりやすいかもしれません。
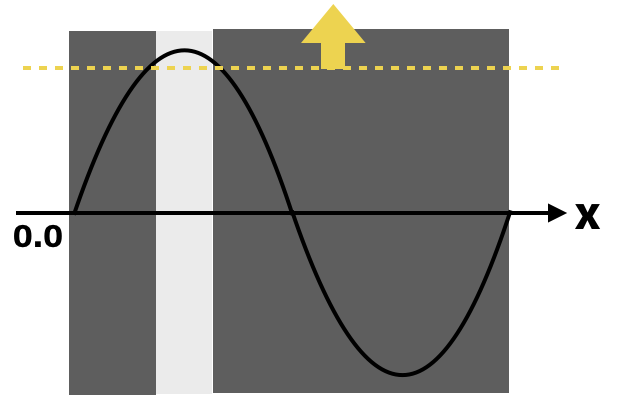
プログラムは次のようになります。
fixed4 frag (v2f i) : SV_Target { fixed len = distance(i.uv, fixed2(0.5,0.5)); return step(0.999, sin(len*4)); }
ここではdistanceで画面中心からの距離をsinの横軸として使っています。sinの頂上だけを切り取るためstep関数を使って、0.99以上なら1が出力されるようにしています。
輪の数を増やす

円の輪郭線を描画するところで、step関数ではなくsin関数を使いました。実はsinを使うとstepよりも簡単に表現の幅を広げることができます。
まずは輪の数を増やしたい場合。これはsinの周波数を高くすることで、山の頂上の数も増え、結果的に輪の数を増やすことができます。
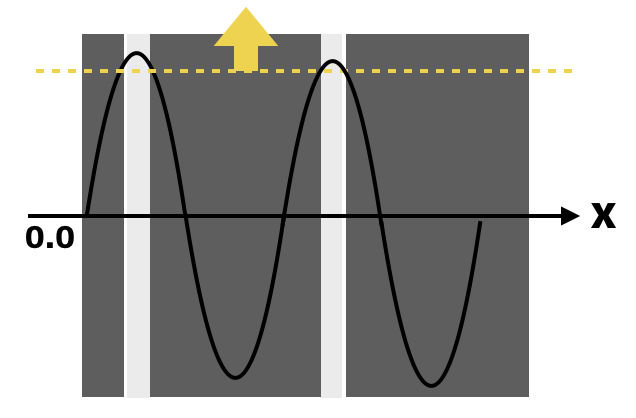
プログラムは次のとおりです。
fixed4 frag (v2f i) : SV_Target { fixed len = distance(i.uv, fixed2(0.5,0.5)); return step(0.9, sin(len*50)); }
frequencyという変数を用意し、これを中心からの距離(sinの横軸方向の値)に掛けています。freqencyの値を増やすことで、輪の数を簡単に増やすことができます。
輪を動かす

輪を動かしたい場合にはsin波を時間とともに動かせば良さそうです。時間とともに移動というと難しそうですが、sin波の引数にオフセットの値として時間を足し合わせるだけです。
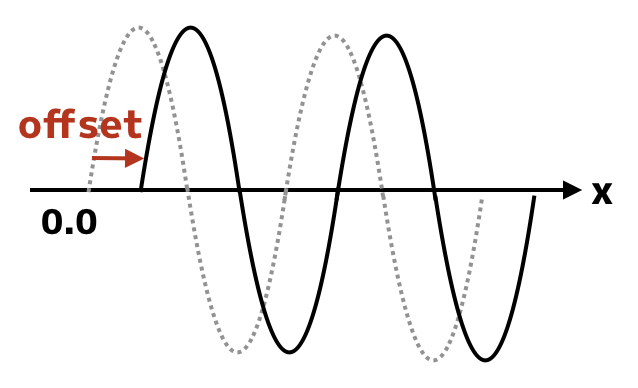
プログラムは次のようになります。
fixed4 frag (v2f i) : SV_Target { fixed len = distance(i.uv, fixed2(0.5,0.5))+_Time; return step(0.9, sin(len*50)); }
sinの中で足している_Time変数はUnityのシェーダに用意されている値で、時間を返します。従って時間が経てばオフセットがどんどん左にずれるため、円が内側に向かって動いているように見えます。
逆に円を外側に向かって動かしたいときは、_Timeを引けばOKです。
ストライプを書く

ストライプ(縞模様)は、上のsin波を使って描くことができます。なんとなく想像がつきますね・・・笑。
次の図ような感じで、x方向に向かうsin波を考えます。今回は頂上付近を取り出すのではなく、0以上なら出力は「1」、0未満なら出力は「0」にします。

プログラムは次のとおりです。
fixed4 frag (v2f i) : SV_Target { return step(0, sin(50*i.uv.x)); }
市松模様を描く

続いて市松模様の描き方です。ストライプが描けたんだから、横向きにもストライプを描けばいいだけでしょ、と思いますが、それだと市松模様ではなくただの格子模様になってしまいます。
一松模様にするための工夫が必要になるわけで、ここが結構面倒です。まずはストライプのときとほとんど同じですが、sinの値が0以下の部分(黒色部分)を0、0以上の部分(白色部分)を0.5で表します。1ではなく0.5なところが味噌です。縦方向も同じように黒を0、白を0.5で表します。
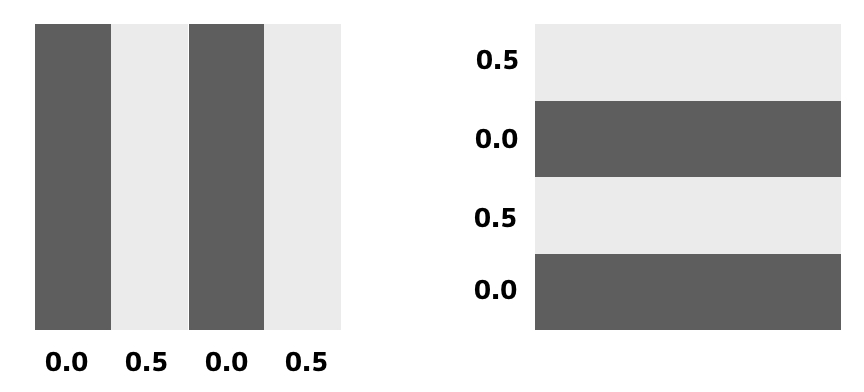
最後に縦方向と横方向の値を足し合わせます。すると、次のように0と0.5と1のマス目ができますね。
このマス目の値に対してfracの演算をします。fracは数値から小数部分を取り出す演算なので、0と1は「0」、0.5は「0.5」になります。これに2を掛けることで「0」と「1」の市松模様ができるわけです。

プログラムは次のようになります。
fixed4 frag (v2f i) : SV_Target { fixed2 v = step(0,sin(50*i.uv))*0.5; return frac(v.x+v.y)*2; }
上のプログラムでは横方向と縦方向の計算を一度に行いvの変数に代入しています。2行目ではx軸の値とy軸の値を足してfrac演算をし、最後に2を書けて市松模様にしています。
四角を描く

四角形は、step関数を使って四角形の周囲4箇所を黒く塗りつぶすイメージです。
(0.5,0.5)を中心に四角形を描くため、まずは左下座標を計算してからstep関数で左半分を塗りつぶします。次に上下左右に反転させて右上部分を塗りつぶせば4隅を黒く塗りつぶすことができます。
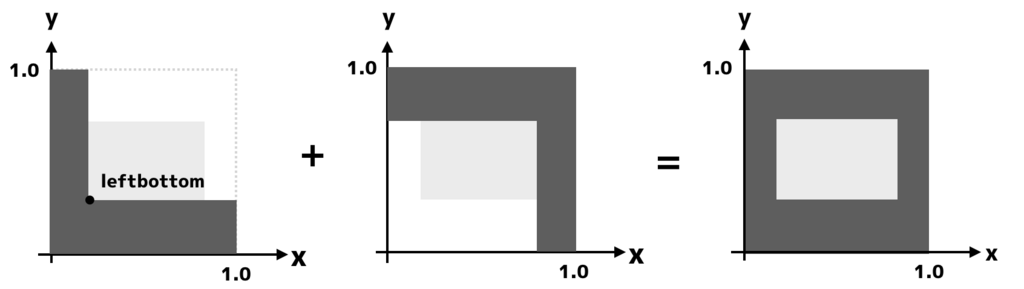
プログラムは次のとおりです。
fixed4 frag (v2f i) : SV_Target { fixed2 size = fixed2(0.3,0.1); fixed2 leftbottom = fixed2(0.5,0.5) - size * 0.5; fixed2 uv = step(leftbottom, i.uv); uv *= step(leftbottom, 1-i.uv); return uv.x*uv.y; }
一行目のsizeは四角形の幅と高さを表します。次に左下座標を計算するため、中心座標から長方形の幅と高さの半分を引いています。
3行目でstep関数を使って四角形の左下部分を塗りつぶしています。また、4行目で1-i.uvとすることで上下左右に反転させて(線の部分でやったのと同じ方法です)四角形の右上部分を塗りつぶしています。
図形を複製してパターンを描画する

最後に図形を複製する方法を紹介します。ここまでは一つの画面に1つの図形を描いてきましたが、上のように同じ図形をの繰り返しパターンを描きたいことがあります。
一つ一つの図形の座標を指定して描画するとなると大変ですが、シェーダを使うととても簡単に図形を増やすことができます。
縦横3x3の図形を描くことを考えてみましょう。ここまで、xとyが0〜1の範囲の正方形の領域に描画してきました。これを、一旦縦横3倍して0~3の範囲に変換します。続いてfracを使うことで0~1の箱が縦横3つ並んでいる状態にします。
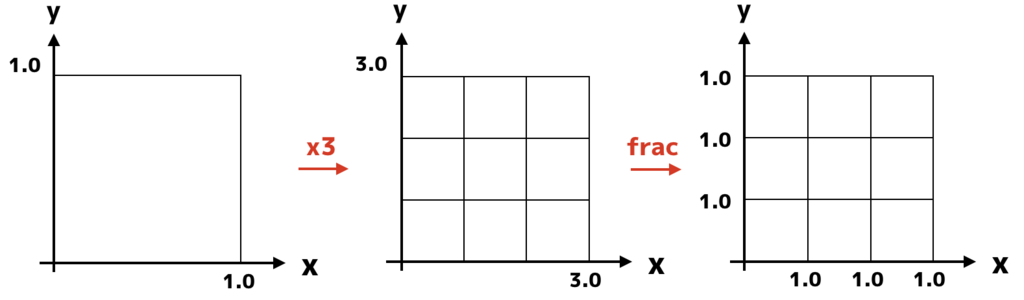
図形の描画は0〜1の範囲に対して行われるので、これだけで図形を複製することができます。
プログラムは次のとおりです。
fixed4 frag (v2f i) : SV_Target { fixed2 st = i.uv * 3; st = frac(st); // 円の描画 fixed l = distance(st,fixed2(0.5,0.5)); return step(0.35, l); }
プログラムでは一旦uv座標を3倍してst変数に代入しています。その後frac関数を使って0〜1のuv座標が3回繰り返すようにしています。あとは、いつもどおりの要領でuvが0〜1の範囲に円を描画しています。

